图形规律推理的四 大命题形式分别是一条式、两组式、九宫格和分组分类。

　　其中分组分类题，要求考生将所给出的六个图形分为两类，使每一类图形都有各自的共同特征或规律，在四组选项中找出正确答案。

　　在做分组分类题的过程中，由于选项是将六个图形的序号进行三比三的分组，所以理论上至多观察四幅图，分类依据就一定能够出现。实际做题过程中，一部分分组分类题差异大、分类依据明显，还有一部分分组分类题的六幅图差异小、共同点明显。想要又快又准地解好分组分类题，需要我们修炼几个针对性的招数，这组招式的名字叫“反义招数”。

　　反义招数第一式，“粗”中有“细”。

　　“粗”指的是粗归类，“细”指的辨细节。 以下面这道题为例：

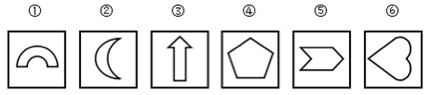
　　【 例 1 】 把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是 ：

　　A. ①③⑥，②④⑤ B. ①③⑤，②④⑥

　　C. ①④⑥，②③⑤ D. ①②④，③⑤⑥

　　粗略观察这道题的前两幅图不难发现，两幅图没有任何相同或相似性，先将考点归类到“数量类或属性类”;进一步观察细节，①图形有端点往外开放，而②图形无端点呈现封闭，则可以考虑开放性。检查完所有图，刚好有端点往外开放的有①④⑥三幅图、无端点呈现封闭的有②③⑤三幅图，答案就出来了，选择 C 选项。

　　反义招数第二式，大“同”小“异”。

　　“同”指的是共同点，“异”指的差异 。如下：

　　【 例 2 】 把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是 ：

　　A. ①②③，④⑤⑥ B. ①③④，②⑤⑥

　　C. ①③⑤，②④⑥ D. ①④⑥，②③⑤

　　六幅图都具备对称性的共同点，但差异在于对称轴方向刚好出现两种：竖向对称轴、横向对称轴。则按对称轴方向检查是否为三比三的数量分布，刚好三比三则答案出现，选择 B 选项。

　　又如：

　　【 例 3 】 把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是 ：

　　A. ①②③，④⑤⑥ B. ①②⑤，③④⑥

　　C. ①②④，③⑤⑥ D. ①③⑥，②④⑤

　　六幅图的共同点是多边形内部都有一个小圆，抓住该共同点进一步找差异，发现小圆仅出现在两种位置：直角处、锐角处。则按小圆位置检查是否为三比三的数量分布，刚好三比三则答案出现，选择 B 选项。