提到容斥 问题 ,大家脑海中是不是出现了“集合”、“画图”的画面,没错, 对于容斥问题 最直观的解决方法的确是找到集合之间的关系,然后画图来解决问题。但是,今天小 编老师 给大家介绍 几种 更为简便的公式法,一 招直接解决容斥 问题。快拿出笔记本记下来啊!
介绍容斥问题 之前,大家可以思考个问题, 什么是容斥原理呢?
所谓容斥原理,就是 在计数的时候,找到 集合 重复的部分并且剔除 掉 的过程 , 使 最终 计 数 的结果既无遗漏又无重复。
先给大家介绍下两个集合的容斥原理:
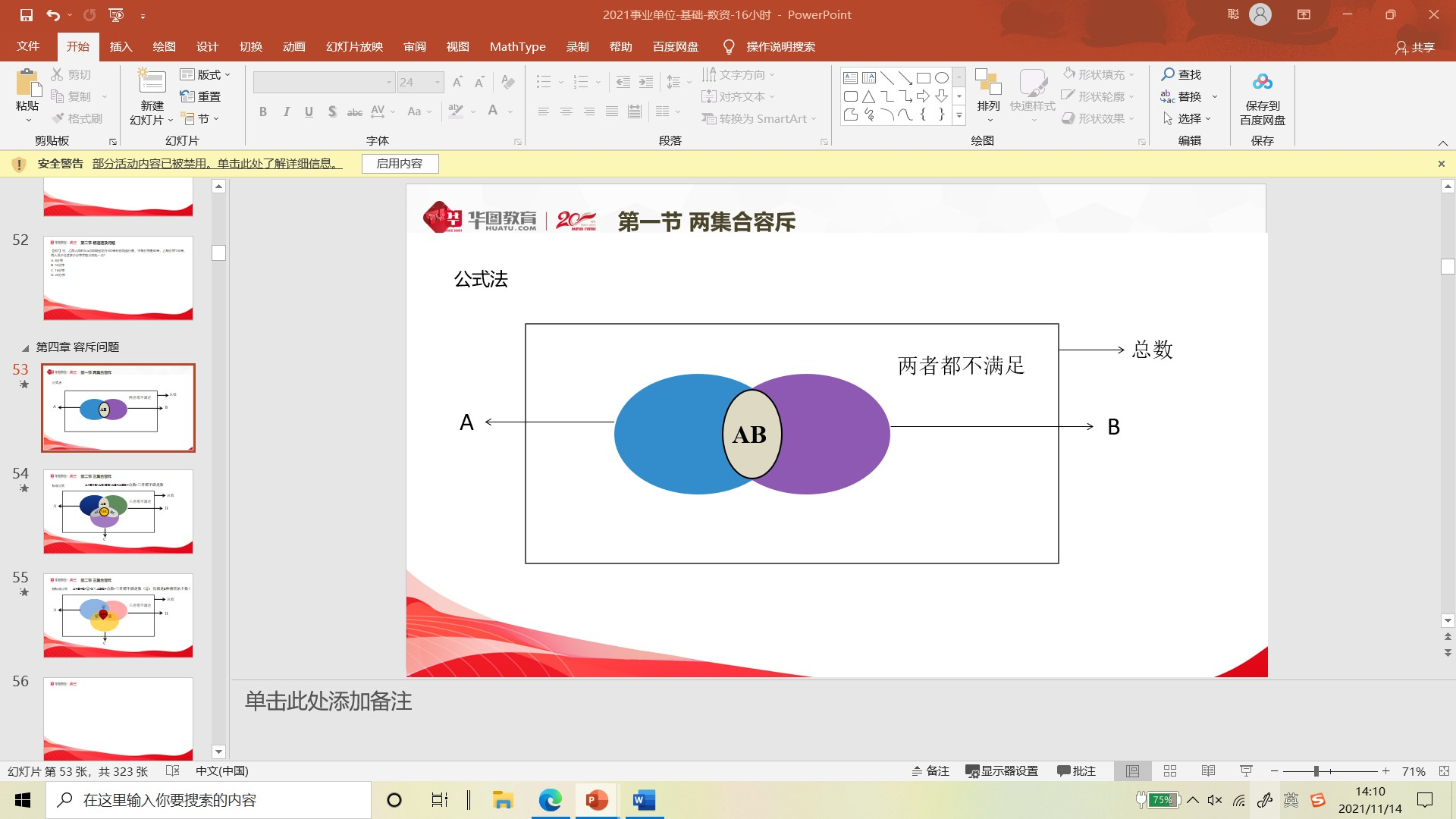
举个小例子:两个集合 A 、 B 分别代表班级中参加篮球小组和足球小组的人数,现在想知道班级中参加篮球和足球小组共有多少人?
通过画图可推出二 集合容斥公式 为: A+B-AB= 总数 - 两者都不满足数 ,在解题时直接用公式计算,这样就会节省每道题画图的时间。 大家一起来练习 一 道题:
【例 1 】某班学生总数为 32 人,第一次参加文娱晚会的有 26 人,第二次参加文娱晚会的有 24 人。若两次文娱晚会中都没有参加的学生有 4 人,则两次都参加文娱晚会的有多少人?
A. 22 B. 18
C. 30 D. 20
【思路点拨】 题干中分成参加两次文娱活动晚会的两个集合, 问的是交叉集合的人数,可以 判定 是容斥问题 。 学生总数为 32 人,第一次参加有 26 人、第二次参加有 24 人、两次都没参加的学生有 4 人,设两次都参加的人数为 x ,代入二 集合 容斥 公式 26 + 24 - x = 32 - 4 ,解得 x = 22 (人) 。 因此,选择 A 选项 。本题较为简单,直接套用公式即可,那接下来给大家介绍三 集合容斥公式 。
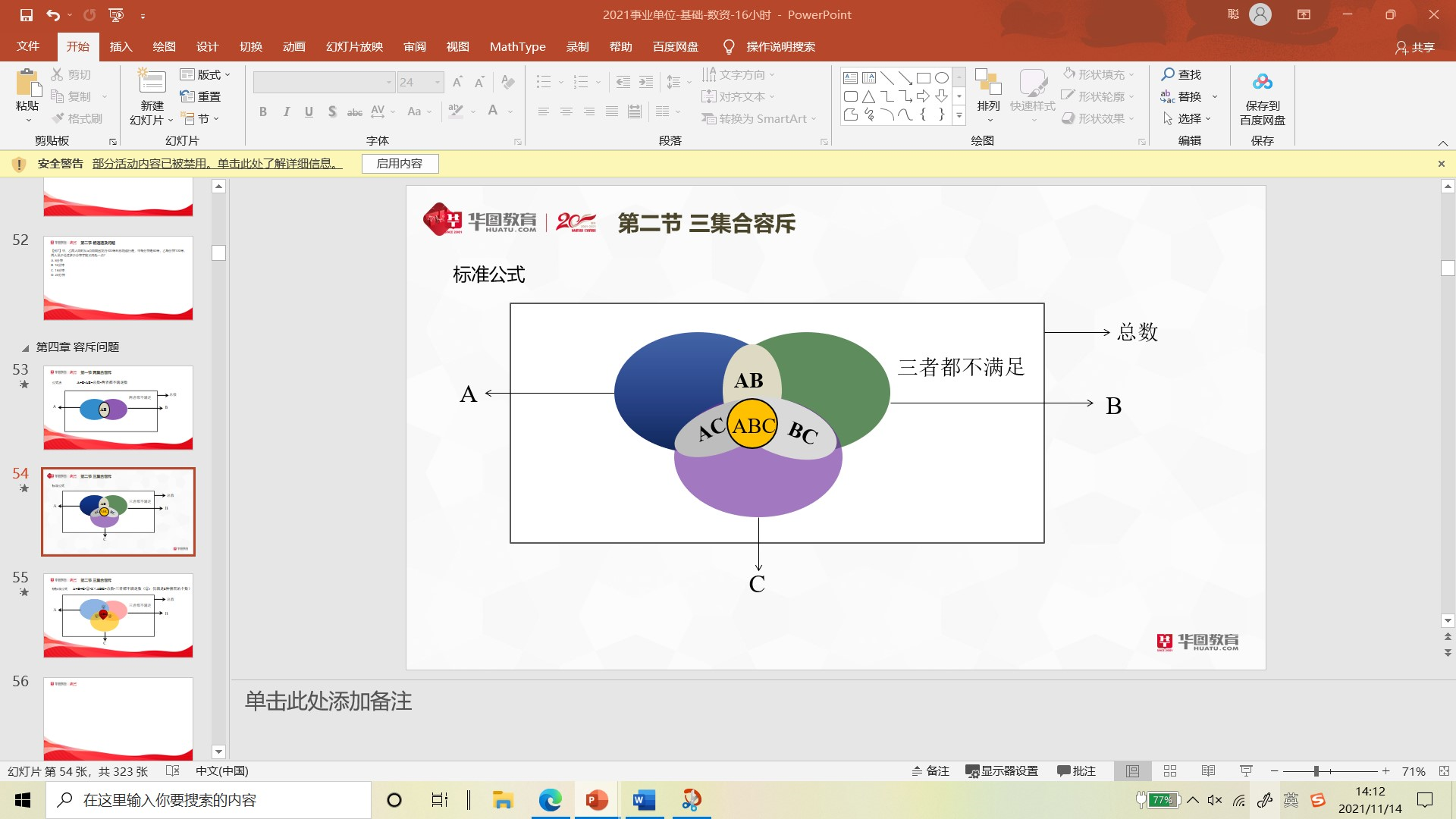
举个小例子:三个集合 A 、 B 、 C 分别代表班级中参加篮球小组、足球小组和羽毛球小组的人数,现在想知道班级中参加三个小组共有多少人?
通过画图可推出三 集合容斥公式 为: A+B+C-AC-BC-AB+ABC= 总数 - 三者都不满足数
大家要注意的是, 三集合和二集合不同点在于,中间 A BC 代表着同时参加三个小组的人数, 因为在减掉 A C 、 B C 、 A B 三个集合时,中间部分减掉了三次,所以 最终要加上同时参加的人数, 一定 不 能 忘记 哦 。 再看 一 道例题:
【例2】 某单位共有 240 名员工,其中订阅 A 期刊的有 125 人,订阅 B 期刊的有 126 人,订阅 C 期刊的有 135 人,订阅 A 、 B 期刊的有 57 人,订阅 A 、 C 期刊的有 73 人,订阅 3 种期刊的有 31 人,此外,还有 17 人没有订阅这三种期刊中的任何一种。问订阅 B 、 C 期刊的有多少人?
A. 57 B. 64
C. 69 D. 78
【思路点拨】 题干中订购 A 、 B 、 C 三种期刊,也就意味着三个集合,即 本题考查 三集合 容斥原理。应用三集合标准型容斥原理公式解题。设订阅 B 、 C 期刊的有 x 人, 代入三集合公式, 可列方程: 125 + 126 + 135 - 57 - 73 - x + 31 = 240 - 17 ,解得 x = 64 。因此,选择 B 选项。
在考试中 遇到容斥问题 , 只要能够识别出题目是考查 集合容斥问题 ,直接用公式解题就会很简单,希望今天的分享能够帮助到大家,大家要继续加油努力 吖 !